Functions III
Anonymous.
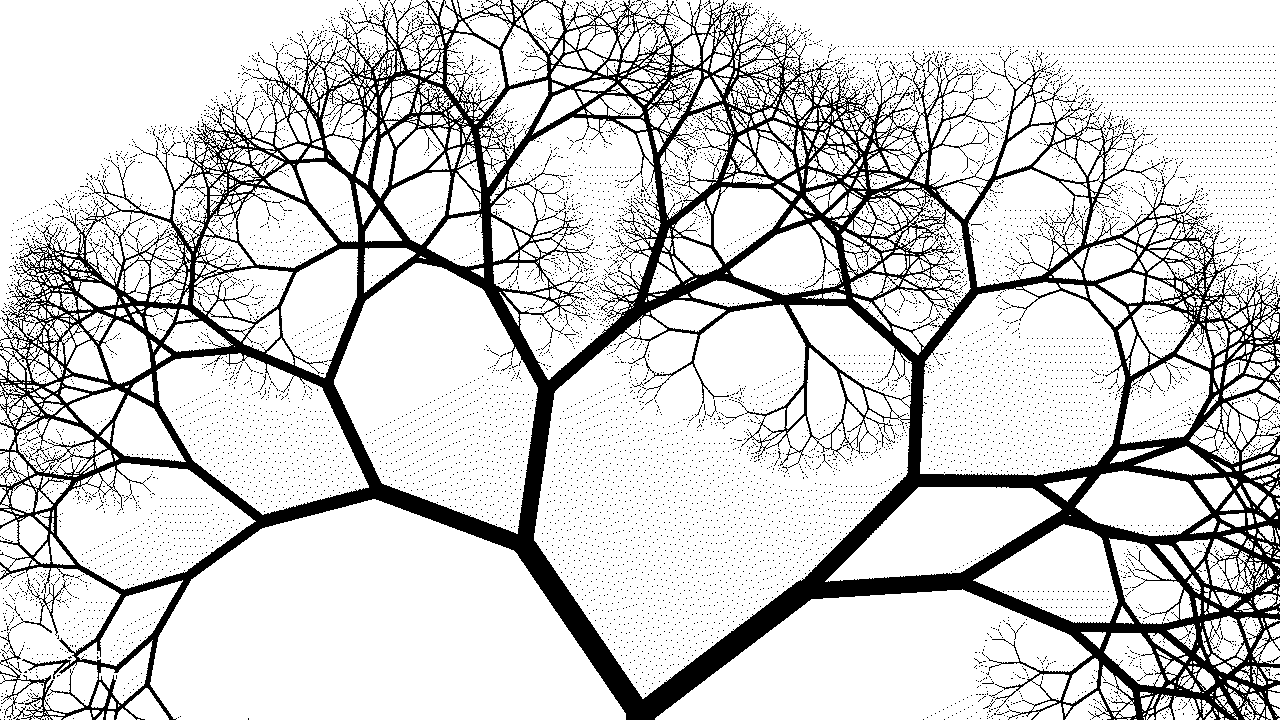
Lindenmayer Fractal System.
How many branches in a tree?
There is a special use of functions that we call recursion and which merits some explanation. We can simply define recursion in programming as a function that calls itself. That is to say we repeat the same function within its structure but with a slight difference on each iteration. This may seem strange at first but is a perfectly acceptable use of functions. The concept of self-reference is a powerful means of generating complex form. If you want a direct visual understanding of recursion, then fractals are where you want to go and learn more. This fascinating field of study is a wealth of recursive applications.
Why would we want to use recursion though, apart from making psychedelic infused graphics? Well, it's an elegant solution for generating some interesting sequences of values, some of which are quite famous like the Fibonnaci sequence. Elegant because it is efficient and with efficiency comes speed. For exmaple, recursion is an integral part of a many famous sorting algorithms which enable sorting a list of elements into ascending/descending order with considerable ease.
Caution is needed in writing recursive functions, namely in avoiding what is called stack overflow. If we are making a call to a function within that function, it goes without saying that we are in a loop like behaviour. It is important then that we create a means for exiting this infinite loop. Otherwise we will end up crashing the program and probably the computer too. To begin, let's look at a relatively simple example that draws a fractal of circles.
There are four main steps to a recursive function: 1). We declare a function, giving it a name and eventually its parameters. 2). We define our function within curly brackets - the body. 3). We call our function within the function. 4). We have a means to exit this call - usually with a condition.
Eg 2. java
void
drawCircle
(float _x, float _y, float _radius)
{
strokeWeight(0.5);
ellipse(_x, _y, _radius/2, _radius/2);
if (_radius > 12.0) { // note the condition
_radius *= 0.95;
drawCircle(_x+_radius/2, _y, _radius/2);
drawCircle(_x-_radius/2, _y, _radius/2);
drawCircle(_x, _y+_radius/2, _radius/2);
drawCircle(_x, _y-_radius/2, _radius/2);
}
}
A recursive function is syntactically the same proceedure as a normal function. So we have our declaration with a name and arguments and the body that includes the definition.
What differs is that we are making a call to this very function within itself. In this case, we are calling four times the same function. Look carefully at what we are doing within those self-referential calls. We are dividing the value of the radius on each iteration but we are also multyplying that value by 0.95 and hence making it smaller on each call.
Also take note of the conditional control structure. For as long as the radius value is greater than 12 pixels, we execute the five lines of code: decreasing the value of the radius on each iteration & drawing four more ellipses. That if statement is important as it enables the program to exit the recursive proceedure. Without which we'd go into the infinite loop of hell. Try playing with that value of 12 pixels and observe what happens.
In the example, recursion_02, we implement a well known algorithm called the Lindenmayer system or L-System which simulates branch like structures. The code is a little more complicated but the main principles remain; a call to the function within itself and a control structure to exit the recursive call. L-Systems are part of a number of fractal geometries that are fascinating to explore. Fractals are the foundations for a whole branch of physics too, in line with symmetry and lots of egg head stuff.